Методы определения сечения проводов электрических сетей

В данной статье будут рассматриваться различные методы определения сечения проводов линии электрических сетей, на примере расчета линии электропередач напряжением 35 кВ.

Содержание

• 1. Метод постоянного сечения вдоль линии
• 2. Метод минимальной затраты металла
• 3. Метод минимума потерь
• 4. Определение сечения по методу экономической плотности тока
• 5. Сравнение методов по затратам металла, потерям мощности и электроэнергии
• 6. Оценка методов определения сечения проводов ВЛ

Исходные данные:

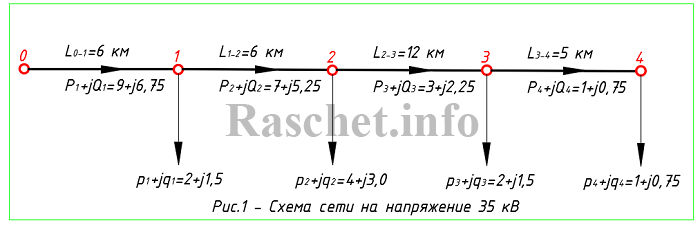
Схема сети на напряжение 35 кВ изображена на рис.1.

• Время использования максимальной нагрузки для всех потребителей Тmax = 2500 ч и Тmax = 6000 ч;
• Сеть выполняется сталеалюминевыми проводами, расстояние между проводами 3000 мм, расположенные – по треугольнику;
• Коэффициент мощности cosϕ = 0,8;
• На схеме, нагрузки выражены в МВт и Мвар, а длины участков в км. Полная мощность записана в виде комплексной полной мощности: Ṡ = P+jQ.

Например, для первого участка комплексная полная мощность равна: Ṡ = p1 + jq1 = 2 +j1,5.

При этом полная мощность определяется как модуль комплексной полной мощности:

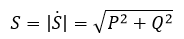
Решение:

1. Допустимая потеря напряжения, принята согласно [Л1, с.119], составляет:

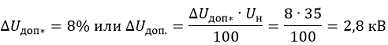
2. Определяем мощности по участкам и результаты наносим на схему рис.1:

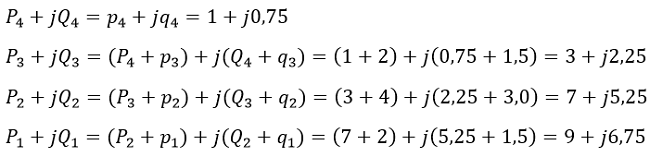
Так как величина реактивного сопротивления линии х0 на 1 км изменяется в зависимости от сечения провода незначительно. Согласно [Л1, с.143] величина реактивного сопротивления составляет:

• для воздушных линий в пределах от 0,36 до 0,46 Ом/км;
• для кабелей напряжением 6-10 кВ – от 0,06 до 0,09 Ом/км;
• для кабелей напряжением 35 кВ – от 0,11 до 0,13 Ом/км.

Поэтому для упрощения расчетов, принимаем среднюю реактивность воздушной линии напряжением 35 кВ равную х0 = 0,4 Ом/км.

3. Определяем допустимую потерю напряжения, обусловленную реактивными сопротивлениями по формуле 6-35 [Л1, с.143]:

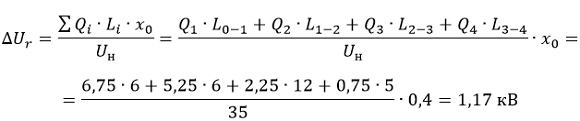
где:

• Uн =35 кВ – номинальное напряжение сети;
• х0 = 0,4 Ом/км – среднее реактивное сопротивление воздушной линии на напряжение 35 кВ;
• Q – реактивная мощность участка, МВАр;
• L – длина участка, км.

4. Определяем допустимую потерю напряжения, обусловленную активной составляющей нагрузки при заданной допустимой потери напряжения ΔUдоп. = 2,8 кВ по формуле 6-36 [Л1, с.143]:

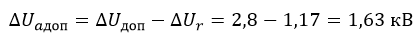
1. Метод постоянного сечения вдоль линии

1.1. Определяем сечение провода на всей длине линии по формуле 6-37 [Л1, с.144]:

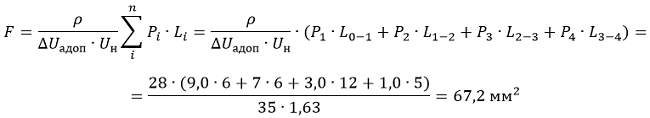
где:

• P – активная мощность участка, МВт;
• L – длина участка, км;
• ρ = 0,028 Ом*мм2/м = 28 Ом*мм2/км – удельное сопротивление материала жилы при 20 °С (температура изготовления жилы) для алюминия [Л2, с.30].

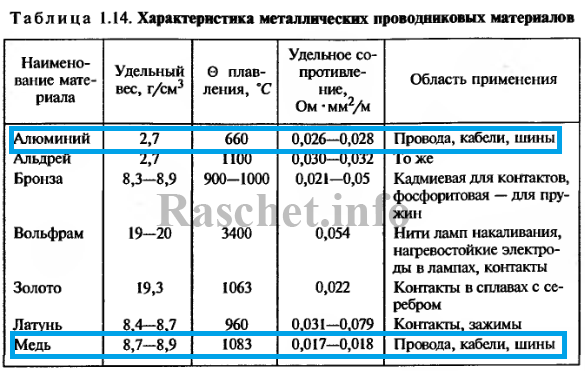
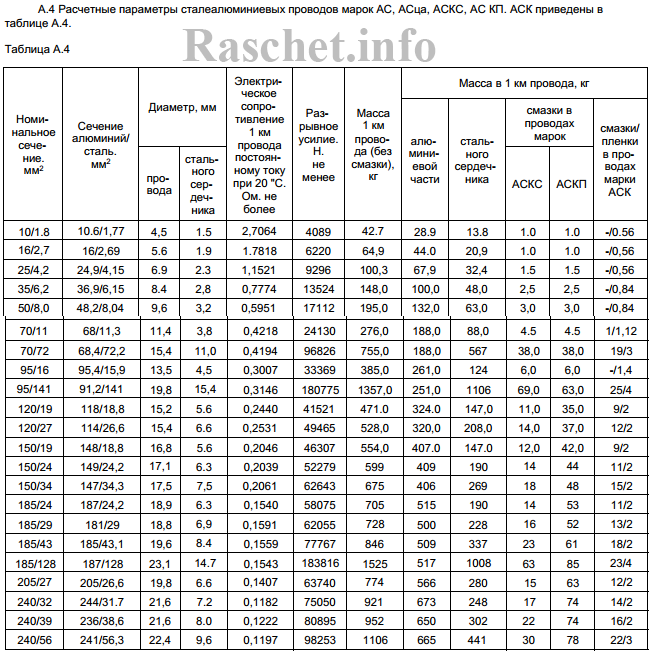
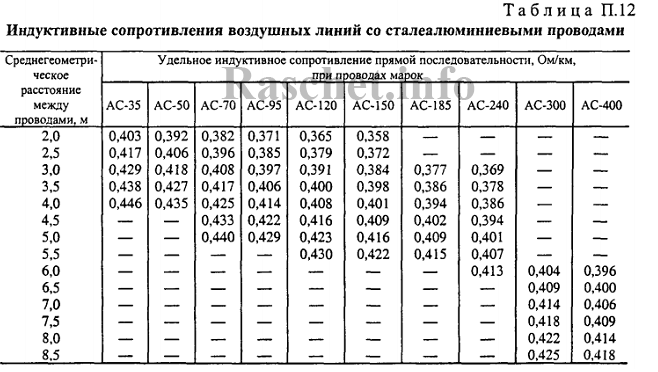
Предварительно принимаем провод марки АС-70 для всей линии. Для данного провода активное и индуктивное сопротивление равно r0 = 0,421 Ом/км, x0 = 0,408 Ом/км; см. ГОСТ 839 таблица А.4 и РД 153-34.0-20.527-98 таблица П12 при среднегеометрическом расстоянии между проводами 3,0 м.

1.2. Определяем фактическую потерю напряжения по формуле 6-35 [Л1, с.143]:

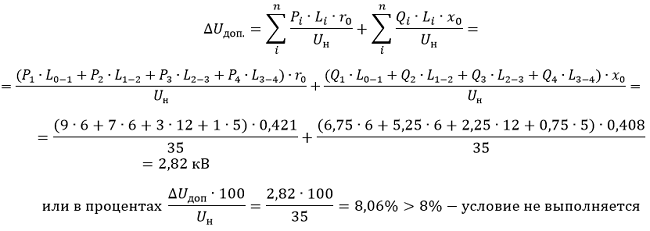
1.3. Определяем фактическую потерю напряжения для провода АС-95, где: r0 = 0,314 Ом/км, x0 = 0,397 Ом/км:

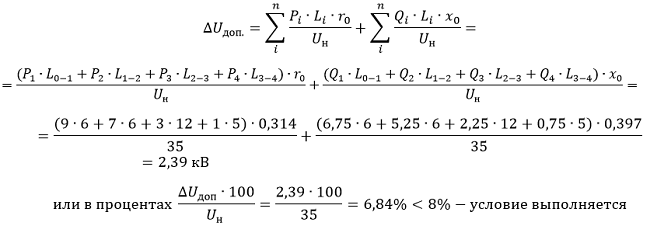
2. Метод минимальной затраты металла

2.1. Определяем коэффициент kр по формуле 6-39 [Л1, с.145]:

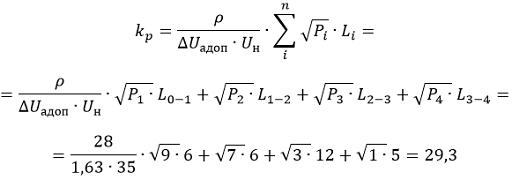
2.2. Определяем сечение проводов для каждого участка, по формуле 6-40 [Л1, с.146]:

2.3. Определяем активные и индуктивные сопротивления для выбранных проводов по ГОСТ 839 таблица А.4 и РД 153-34.0-20.527-98 таблица П12 при среднегеометрическом расстоянии между проводами 3,0 м:

• АС-35: r0 = 0,777 Ом/км, x0 = 0,429 Ом/км;
• АС-50: r0 = 0,595 Ом/км, x0 = 0,418 Ом/км;
• АС-95: r0 = 0,314 Ом/км, x0 = 0,397 Ом/км;

2.4. Проверяем потерю напряжения по формуле 6-35 [Л1, с.143] с учетом выбранных марок проводов:

3. Метод минимума потерь

Рассмотрим условия выбора сечения линии, исходя из требования минимальных потерь мощности.

Условием минимальных потерь в линии является постоянство плотности тока на всех участках. Величину плотности тока, соответствующую минимуму потерь, определяют по допустимой потере напряжения ΔUaдоп., обусловленной активным сопротивлением.

3.1. Определяем плотность тока, соответствующая минимальным потерям по формуле 6-43 [Л1, с. 147]:

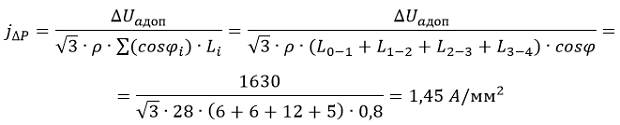
где:

• P – активная мощность участка, МВт;
• L – длина участка, км;
• ρ = 0,028 Ом*мм2/м = 28 Ом*мм2/км – удельное сопротивление материала жилы при 20 °С (температура изготовления жилы) для алюминия [Л2, с.30];
• ΔUaдоп = 1630 В — допустимая потеря напряжения, обусловленная активной составляющей нагрузки, рассчитанная ранее в данной статье.

3.2 Определяем рабочие токи в каждом участке по формуле [Л1, с.129]:

3.3. Определяем сечение проводов по формуле 6-44 [Л1, с.147]:

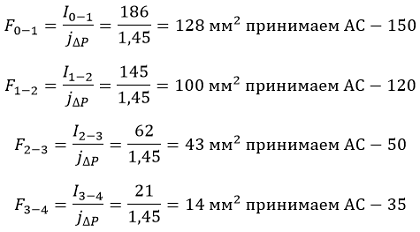
3.4. Определяем активные и индуктивные сопротивления для выбранных проводов по ГОСТ 839 таблица А.4 и РД 153-34.0-20.527-98 таблица П12:

• АС-35: r0 = 0,777 Ом/км, x0 = 0,429 Ом/км;
• АС-50: r0 = 0,595 Ом/км, x0 = 0,418 Ом/км;
• АС-120: r0 = 0,244 Ом/км, x0 = 0,391 Ом/км;
• АС-150: r0 = 0,204 Ом/км, x0 = 0,384 Ом/км;

3.5. Проверяем потерю напряжения по формуле 6-35 [Л1, с.143] с учетом выбранных сечений:

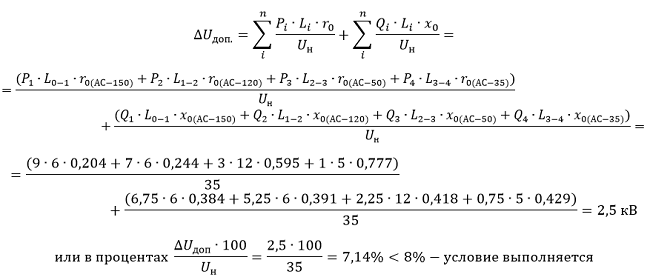
4. Определение сечения по методу экономической плотности тока

4.1. Определяем экономическое сечение проводов по участкам, согласно ПУЭ п. 1.3.25, с учетом что Тmax= 2500 ч:

где:

• I – расчетный ток участков, А;
• Jэк = 1,3 — нормированное значение экономической плотности тока (А/мм2) для неизолированных алюминиевых проводов выбираем по ПУЭ таблица 1.3.36, с учетом что время использования максимальной нагрузки Тmax= 2500 ч.

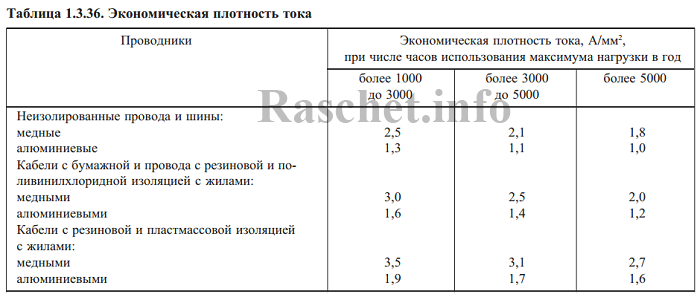
4.2. Определяем экономическое сечение проводов по участкам, согласно ПУЭ п. 1.3.25, с учетом что Тmax= 6000 ч:

где: Jэк = 1,0 — нормированное значение экономической плотности тока (А/мм2) для неизолированных алюминиевых проводов выбираем по ПУЭ таблица 1.3.36, с учетом что время использования максимальной нагрузки Тmax= 6000 ч.

4.3. Определяем активные и индуктивные сопротивления для выбранных проводов при среднегеометрическом расстоянии между проводами 3,0 м:

• АС-35: r0 = 0,777 Ом/км, x0 = 0,429 Ом/км;
• АС-70: r0 = 0,421 Ом/км, x0 = 0,408 Ом/км;
• АС-150: r0 = 0,204 Ом/км, x0 = 0,384 Ом/км;
• АС-185: r0 = 0,154 Ом/км, x0 = 0,377 Ом/км;

4.4. Проверяем потерю напряжения по формуле 6-35 [Л1, с.143] с учетом выбранных сечений:

5. Сравнение методов по затратам металла, потерям мощности и электроэнергии

5.1. Определяем затраты металла по каждому участку и результаты по вариантам сведем в таблицу 1. Данные о массе 1 км провода принимаем согласно ГОСТ 839 таблица А.4.

Таблица 1 – Затраты цветного металла

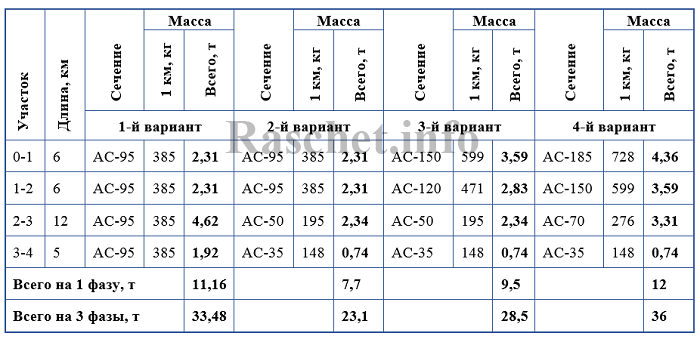
Как мы видим, наименьшие затраты металла получились во 2-м варианте, рассчитанном по методу минимальной затраты металла.

5.2. Определяем потери активной мощности на участках трехфазной линии с активным сопротивлением r0 по формуле 4-1а [Л1, с.74]:

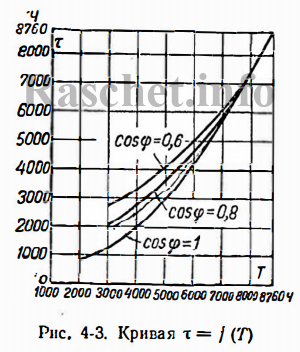
5.3. Определяем время максимальных потерь (τ), исходя из коэффициента мощности cosϕ=0,8 и время использования максимальной нагрузки Тmax= 2500 ч и Тmax= 6000 ч, согласно рис.4.3 [Л1, с.78]:

• для Тmax= 2500 ч – τ = 1600 ч;
• для Тmax= 6000 ч – τ = 4500 ч.

5.4. Определяем потери электроэнергии по формуле [Л1, с.151]:

Результаты расчетов по всем вариантам заносим в таблицу 2.

Таблица 2 – Потери мощности и электроэнергии

Участок	Варианты
	1-й	2-й	3-й	4-й
Потери мощности, кВт
0-1	196	196	127	96
1-2	119	119	92	77
2-3	43,4	82	82	58
3-4	2	5	5	5
Итого:	360	401,8	306,9	236,5
Потери электроэнергии, кВт*ч 103
При τ = 1600 ч	576	643	491	378
При τ = 4500 ч	1620	1808	1381	1064

Минимальные потери получились в 3-м и 4-м вариантах, т.е. при расчетах, выполненных по методу минимума потерь и по методу экономической плотности тока.

Вывод:

Как видно из результатов расчета 1-й вариант, определенный по методу постоянного сечения вдоль линии, неприемлем по всем показателям. Что касается остальных вариантов, то в рассмотренном примере они по своим показателям близки друг к другу. Это объясняется прежде всего тем, что сечение проводов на последнем участке выбрано выше требуемого электрическими расчетами по механическим соображениям и поэтому в электрическом отношении использовано не полностью.

6. Оценка методов определения сечения проводов ВЛ

Методы определения сечения проводов электрических сетей по минимуму расхода проводникового материала и по минимуму потерь мощности дают более экономичные решения, нежели те, которые получаются при выборе одинакового сечения по всей длине линии [Л1, с.148].

Первый из упомянутых методов экономит капитальные затраты и соответствующие составляющие эксплуатационных расходов, зависящие от стоимости сооружения линии, и поэтому может применяться для потребителей с малым числом часов использования максимальной нагрузки и для промышленных нагрузок с малыми токовыми нагрузками при незначительных величинах времени потер.

Для потребителей с большим числом часов использования максимума и большими нагрузками целесообразнее пользоваться вторым методом (метод минимальной затраты металла), так как в этом случае прежде всего добиваются уменьшения составляющей эксплуатационных расходов, зависящий от потерь в линии.

Определение сечений проводов по экономическим плотностям тока, установленным ПУЭ, учитывают оба фактора (как экономию капитальных затрат, так и снижение потерь), поскольку экономическая плотность тока принимается в зависимости от времени использования максимальной нагрузки.

Однако при большой протяженности линии сечение проводов, выбранное по экономической плотности тока, может не обеспечить допустимой потери напряжения, что сделает необходимым повторный расчет. Чтобы избежать пересчета, предварительно определяют плотность тока jΔр, обеспечивающую допустимую потерю напряжения. Если окажется, что jΔр > jэ, то принимают сечение по экономической плотности тока, т.е. по jэ. В противном случае сечение выбирают по jΔр.

Значительное превышение выбранного сечения над экономическим свидетельствует о том, что необходимо применить для сети более высокое номинальное напряжение (например, 10 кВ вместо 6 кВ), либо прибегнуть к специальным методам снижения потерь напряжения, например, к компенсации реактивной мощности или к продольной компенсации.

Литература:

1. Электрические сети энергетических систем. В.А. Боровиков. 1977 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.