Пример определения потери напряжения в линии 10 кВ

В данной статье я буду рассматривать 2 примера определения потери напряжения в воздушной линии 10 кВ, когда нагрузка подключена в конце линии и с несколькими нагрузками вдоль линии.

Пример 1 – Определение потери напряжения, когда нагрузка подключена в конце линии

Определить потерю напряжения в трехфазной воздушной линии с номинальным напряжением Uном.=10 кВ протяженностью l = 2 км, питающей электрооборудование коммунального предприятия мощностью Р=100 кВт. Коэффициент мощности нагрузки cosϕ = 0,8. Линия выполнена алюминиевыми проводами марки А-25 сечением 25 мм2, расстояние между фазами 600 мм.

Решение.

1. Определяем активное сопротивление провода марки А-25:

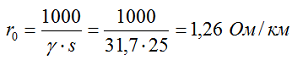
где:

• γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
• s – номинальное сечение провода(кабеля),мм2;

Также вы можете встретить в тех. литературе еще одну формулу по определению активного сопротивления провода (кабеля):

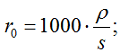
где:

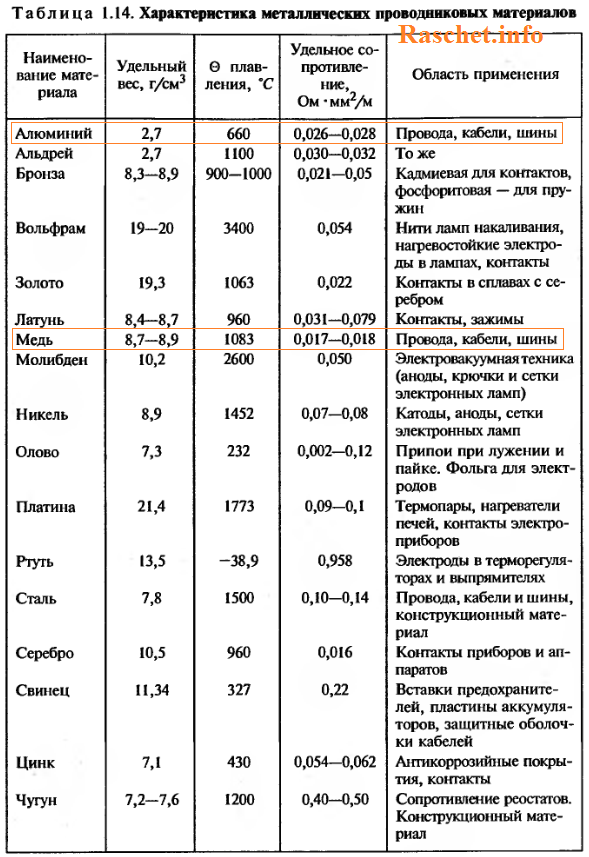
• ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].
  

2. Определяем индуктивное сопротивление для провода марки А-25 [Л1.с.420]:

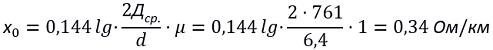
где:

• Дср. – среднее геометрическое расстояние между осями проводов, мм;
• d = 6,40 мм – диаметр провода, для марки провода А-25. Значение диаметра провода можно определить по ГОСТ 839-80  – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. В данном расчете я привожу значение диаметра провода, только для провода марки А, для остальных марок проводов значения диаметров проводов вы сможете найти непосредственно в самом ГОСТе;
• µ — относительная магнитная проницаемость для цветных металлов (немагнитных) равна 1, для стальных проводов µ может достигать значений 10³ и даже больше.

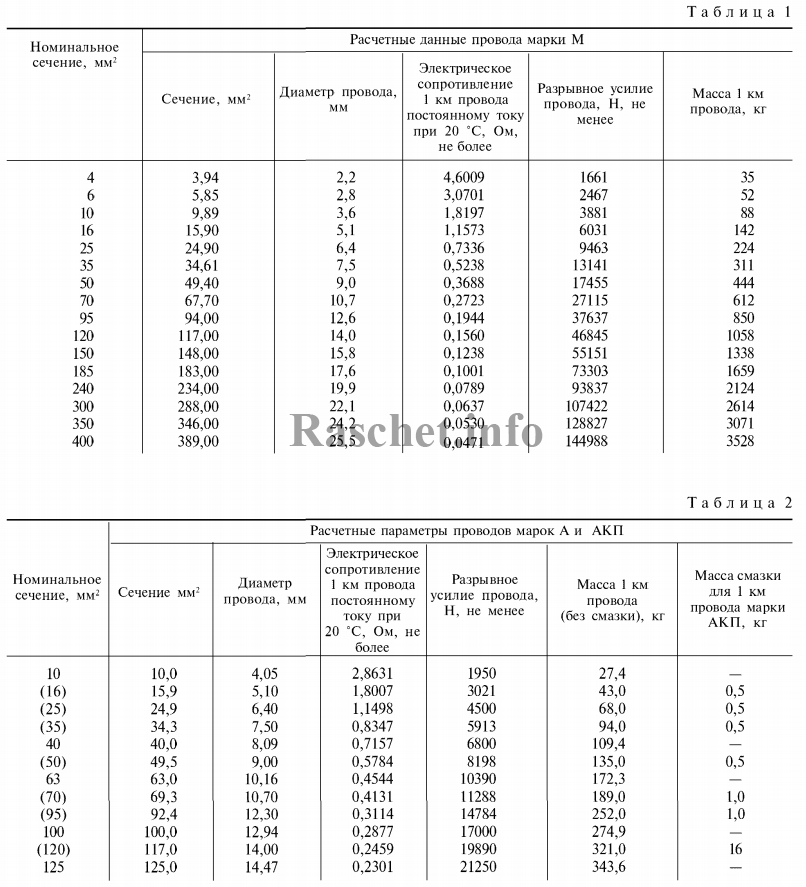
2.1 Определяем среднее геометрическое расстояние между осями трех проводов проложенных в одной плоскости [Л1.с.419]:

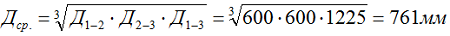
где: расстояние между проводами первой и второй фазы Д1-2= 600 мм, между второй и третью Д2-3 = 600 мм, между первой и третью Д1-3= 600 + 25 + 600 = 1225 мм.

3. Определяем коэффициент мощности tgϕ, зная cosϕ:

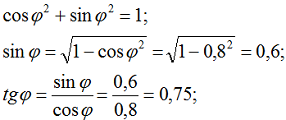
4. Определяем потерю напряжения в линии [Л1.с.422]:

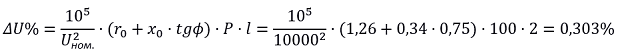
Пример 2 – Определение потери напряжения с несколькими нагрузками вдоль линии

Определить потерю напряжения в трехфазной сети 10 кВ, изображенной на рис.1. Сеть выполнена воздушной линией с алюминиевыми проводами марки А-35 сечением 35 мм2 на участке А-Б и проводами марки А-25 сечением 25 мм2 на участке Б-В. Расстояние между фазами равно 600 мм. Соответствующая нагрузка, коэффициент мощности cosϕ в ответвлениях, а также длины участков сети указаны на схеме.

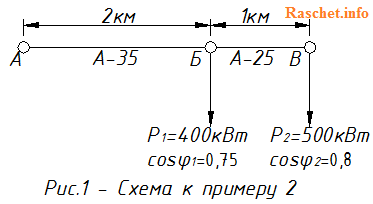
Решение.

1. Определяем активное сопротивление провода марки А-35 на участке А-Б:

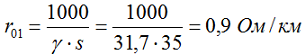
2. Определяем индуктивное сопротивление для провода марки А-35 [Л1.с.420]:

2.1 Определяем среднее геометрическое расстояние между осями трех проводов проложенных в одной плоскости [Л1.с.419]:

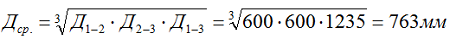
где: расстояние между проводами первой и второй фазы Д1-2= 600 мм, между второй и третью Д2-3 = 600 мм, между первой и третью Д1-3= 600 + 35 + 600 = 1235 мм.

3. Определяем коэффициент мощности tgϕ1, зная cosϕ1:

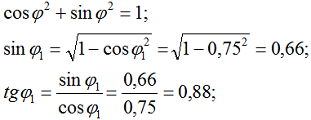
4. Значения активного и индуктивного сопротивления для марки провода А-25 берем из примера 1: r₀₂ = 1,26 Ом/км; х₀₂ = 0,256 Ом/км; tgϕ₂ = 0,75.

5. Определяем суммарную потерю напряжения в линии 10 кВ [Л1.с.422] :

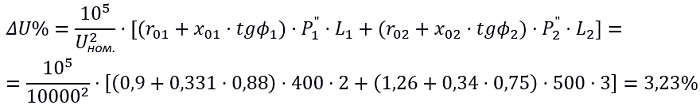
где:

• Uном. – номинальное напряжение, В;
• r₀₁, x₀₁, r₀₂, x₀₂ – активные и индуктивные сопротивления трехфазных линий, Ом/км;
• Р1,Р2 – мощности в ответвлениях, кВт;
• L₁,L₂ – длины от начала линии до соответствующего ответвления, км;
• tgϕ₁, tgϕ₂ – коэффициент мощности;
  

Литература:

1. Основы проектирования систем электроснабжения. Маньков В.Д. 2010 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.